문제
Given a 2D matrix matrix, handle multiple queries of the following type:
- Calculate the sum of the elements of matrix inside the rectangle defined by its upper left corner (row1, col1) and lower right corner (row2, col2).
Implement the NumMatrix class:
- NumMatrix(int[][] matrix) Initializes the object with the integer matrix matrix.
- int sumRegion(int row1, int col1, int row2, int col2) Returns the sum of the elements of matrix inside the rectangle defined by its upper left corner (row1, col1) and lower right corner (row2, col2).
2D 매트릭스가 주어지면 다음 유형의 여러 쿼리를 처리합니다.
왼쪽 상단 모서리(행 1, col1)와 오른쪽 하단 모서리(행 2, col2)로 정의된 직사각형 내부의 행렬 요소의 합계를 계산합니다.
NumMatrix 클래스를 구현합니다.
NumMatrix(int[][] 행렬) 정수 행렬로 개체를 초기화합니다.
intsumRegion(int row1, intcol1, row2, intcol2) 왼쪽 상단 모서리(row1, col1)와 오른쪽 하단 모서리(row2, col2)로 정의된 직사각형 내부의 행렬 요소의 합계를 반환합니다.
예시
Example 1:
Input
["NumMatrix", "sumRegion", "sumRegion", "sumRegion"]
[[[[3, 0, 1, 4, 2], [5, 6, 3, 2, 1], [1, 2, 0, 1, 5], [4, 1, 0, 1, 7], [1, 0, 3, 0, 5]]], [2, 1, 4, 3], [1, 1, 2, 2], [1, 2, 2, 4]]
Output
[null, 8, 11, 12]
Explanation
NumMatrix numMatrix = new NumMatrix([[3, 0, 1, 4, 2], [5, 6, 3, 2, 1], [1, 2, 0, 1, 5], [4, 1, 0, 1, 7], [1, 0, 3, 0, 5]]);
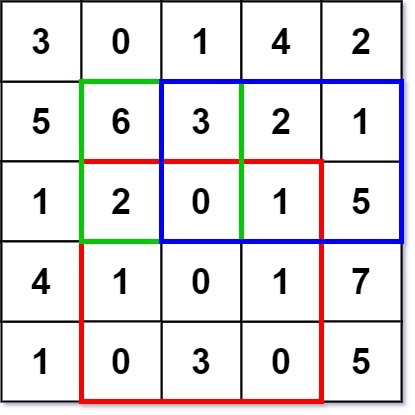
numMatrix.sumRegion(2, 1, 4, 3); // return 8 (i.e sum of the red rectangle)
numMatrix.sumRegion(1, 1, 2, 2); // return 11 (i.e sum of the green rectangle)
numMatrix.sumRegion(1, 2, 2, 4); // return 12 (i.e sum of the blue rectangle)
제약 조건
Constraints:
- m == matrix.length
- n == matrix[i].length
- 1 <= m, n <= 200
- -104 <= matrix[i][j] <= 104
- 0 <= row1 <= row2 < m
- 0 <= col1 <= col2 < n
- At most 104 calls will be made to sumRegion.
해결 코드
/**
* @param {number[][]} matrix
*/
var NumMatrix = function(matrix) {
const m = matrix.length;
const n = matrix[0].length;
const sum = [...Array(m)].map(_ => [...Array(n)].fill(0));
for(let i = 0; i < m; i++) {
for(let j = 0; j < n; j++) {
sum[i][j] = (sum[i - 1]?.[j] || 0) + (sum[i]?.[j - 1] || 0) + matrix[i][j] - (sum[i - 1]?.[j - 1] || 0);
}
}
this.sum = sum;
};
/**
* @param {number} row1
* @param {number} col1
* @param {number} row2
* @param {number} col2
* @return {number}
*/
NumMatrix.prototype.sumRegion = function(row1, col1, row2, col2) {
return this.sum[row2][col2] - (this.sum[row1 - 1]?.[col2] || 0) - (this.sum[row2]?.[col1 -1] || 0) +
(this.sum[row1 - 1]?.[col1 -1] || 0);
};
/*
* Your NumMatrix object will be instantiated and called as such:
* var obj = new NumMatrix(matrix)
* var param_1 = obj.sumRegion(row1,col1,row2,col2)
*/
'leetCode' 카테고리의 다른 글
| [Medium] 138. Copy List with Random Pointer (0) | 2022.07.19 |
|---|---|
| [Medium] 143. Reorder List (0) | 2022.07.19 |
| [Medium] 910. Smallest Range II (0) | 2022.07.15 |
| [Medium] 713. Subarray Product Less Than K (0) | 2022.07.07 |
| [Medium] 438. Find All Anagrams in a String (0) | 2022.07.07 |

Comment